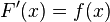
W myśl powyższej definicji całkowanie funkcji 
polega na znalezieniu jej funkcji pierwotnej. Korzystając z alternatywnego zapisu pochodnej funkcji, powyższe równanie przyjmie postać:
polega na znalezieniu jej funkcji pierwotnej. Korzystając z alternatywnego zapisu pochodnej funkcji, powyższe równanie przyjmie postać: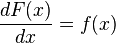
Po obustronnym pomnożeniu przez dx:
Po obustronnym całkowaniu powyższą relację możemy zapisać jako:
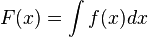
Można zatem powiedzieć z pewnym przybliżeniem, że operacja całkowania jest operacją odwrotną do różniczkowania. Powyższe przybliżenie wynika z faktu, że o ile różniczkowanie jest operacją jednoznaczną, o tyle całkowanie już nie. Funkcja f(x) ma jedną i tylko jedną pochodną f'(x). Natomiast f(x) ma nieskończenie wiele funkcji pierwotych F(x). Mówimy zatem, że wyznaczamy całkę nieoznaczoną funkcji f(x) z dokładnością do stałej addytywnej C, co zapisujemy jako:
